11.手続きと関数

11.手続きと関数

　　手続き宣言　＝　手続き見出し　”;”　指令　｜
　　　　　　　　　　手続き表示　　”;”　手続きブロック　｜
　　　　　　　　　　手続き見出し　”;”　手続きブロック
　　　手続き見出し　＝　”procedure”　名称　［仮引数並び］
　　　手続き表示　　＝　”procedure”　手続き名
　　　手続き名　　　＝　名称
　　　手続きブロック＝　ブロック

　例１）『２数の最大公約数を求める』プログラム

　　PROGRAM rei1(input,output);
　　　VAR a,b,c,d : integer;
　　　　BEGIN
　　　　　READ(a,b);
　　　　　IF a＜b
　　　　　　THEN
　　　　　　　BEGIN　  （１）
　　　　　　　　c:=a;　　｜
　　　　　　　　a:=b;　　｜
　　　　　　　　b:=c　　 ｜
　　　　　　　END;　　 （１）
　　　　　REPEAT
　　　　　　d:=a MOD b;
　　　　　　a:=b;
　　　　　　b:=d
　　　　　UNTIL　d=0;
　　　　　WRITE(a)
　　　　END.

　２変数ａ,ｂを読み込み、最大公約数を求めて、ａに代入し出力するプログラムです。
（注）d:=a MOD b　というのは、ａをｂで割ったときの余りの値をｄに代入するしきのこと。

　　例１の（１）の部分を手続きに直すと次のようなプログラムになります。
　例２）

　　PROGRAM rei2(input,output);
　　　VAR a,b,c,d : integer;
　　　　PROCEDURE okikae;
　　　　　BEGIN
　　　　　　c:=a;
　　　　　　a:=b;
　　　　　　b:=c
　　　　　END;
　　　　BEGIN
　　　　　READ(a,b);
　　　　　IF a＜b
　　　　　　THEN
　　　　　　　okikae;
　　　　　REPEAT
　　　　　　d:=a MOD b;
　　　　　　a:=b;
　　　　　　b:=d
　　　　　UNTIL d=0;
　　　　　WRITE(a)
　　　　END.

　このプログラムからわかること
　　（イ）手続きの宣言は、ブロックの定義・宣言の部分にある。
　　（ロ）手続きの宣言は､プログラムと同じ形をしていて､ただ、「PROGRAM」が「PROCEDURE」に変わっただけである。
　　（ハ）プログラム中に手続きの名前が出てくると、手続きを実行し､実行し終わると、その次にいく。
　　（ニ）プログラムの変数がそのまま手続きの方でも使用できる。
　　（ホ）手続きは何回使われても、宣言は１度でよい。
　例２ではａ,ｂ,ｃ,ｄすべてが大域的変数だったが、次の例３ではａ,ｂ,ｄを大域的変数、ｃを局所的変数としたプログラムを示す。

　例３）

　　PROGRAM rei3(input,output);
　　　VAR a,b,d : integer;
　　　　PROCEDURE okikae;
　　　　　VAR c : integer;
　　　　　　BEGIN
　　　　　　　c:=a;
　　　　　　　a:=b;
　　　　　　　b:=c
　　　　　　END;
　　　　BEGIN
　　　　　READ(a,b);
　　　　　IF a＜b
　　　　　　THEN
　　　　　　　okikae;
　　　　　REPEAT
　　　　　　d:=a MOD b;
　　　　　　a:=b;
　　　　　　c:=d
　　　　　UNTIL d=0;
　　　　　WRITE(a)
　　　　END.

　例３と例２との違いは、変数ｃの扱いである。
　例２では、変数ｃは大域的変数といい、プログラムの中も、手続きの中でも有効であったが、例３では、変数ｃは局所的変数といい、変数ｃを宣言した手続きの中でだけ有効で、その手続きの中以外では変数ｃは存在しない。

　今度は、もう少し高度に、仮引数がある手続きについて述べる。
　　手続き見出し　＝　”PROCEDURE”　名称　［仮引数並び］
　　　仮引数並び　＝　”(”　仮引数区域　｛”;”仮引数区域　｝　”)”
　　　仮引数区域　＝　値引数仕様　｜　変数引数仕様　｜　手続き引数仕様　｜　関数引数仕様　｜　整合配列引数仕様
　　　値引数仕様　＝　名称並び　”:”　型名
　　　変数引数仕様　＝　”VAR”　名称並び　”:”　型名
　　　手続き引数仕様　＝　手続き見出し
　　　関数引数仕様　＝　関数見出し
　　　整合配列引数仕様　＝　変数整合配列仕様　｜　値整合配列仕様
　　　変数整合配列仕様　＝　”VAR”　名称並び　”:”　整合配列形式
　　　整合配列形式　＝　詰めあり整合配列形式　｜　詰めなし整合配列形式
　　　詰めなし整合配列形式　＝　”ARRAY””[”添字型仕様｛”:”添字型仕様｝”]”"OF”（型名　｜　整合配列形式）
　　　詰めあり整合配列形式　＝　”PACKED”　”ARRAY””[”添字型仕様”]””OF”型名

　例３の手続きを、手続き見出しに仮引数並びがあるものに変更してみます。

　例４）

　　PROGRAM rei4(input,output);
　　　VAR a,b,c,d : integer;
　　　PROCEDURE okikae(VAR x,y : integer);
　　　　VAR z : integer;
　　　　　BEGIN
　　　　　　z:=x;
　　　　　　x:=y;
　　　　　　y:=z
　　　　　END
　　　BEGIN
　　　　READ(a,b);
　　　　IF a＜b
　　　　　THEN
　　　　　　okikae(a,b);
　　　　REPEAT
　　　　　　d:=a MOD b;
　　　　　　a:=b;
　　　　　　c:=d
　　　　　UNTIL d=0;
　　　　　WRITE(a)
　　　　END.

　例４の解説
　　手続きに仮引数をつけることにより、繰り返し処理ができる置き換え機能を備えている。すなわち、プログラムから手続きを参照する時に、プログラムからの変数の値を、手続きで局所的変数にその値を入れてプログラムのどの変数にも対応できるようにしている。
　　仮引数の前に「VAR」をつけるかつけないかの違いは、つける時には「変数の置き換え」、つまり、手続きが結果を持ち帰らせる変数で、つけない時は、「値の置き換え」、つまり、手続きが結果を持ち帰らせない変数の違いです。
　　例４の
　　　　　　d:=a MOD b;
　　　　　　a:=b;
　　　　　　c:=d
　の所を仮引数を使った手続きでプログラムを書いてみると、次のようになる。

　例５）

　　PROGRAM rei5(input,output);
　　　VAR a,b : integer;
　　　PROCEDURE okikae(x,y : integer);
　　　　VAR z : integer;
　　　　　BEGIN z:=x; x:=y; y:=z END;
　　　PROCEDURE amari(VAR k,l : integer);
　　　　VAR m : integer;
　　　　　BEGIN
　　　　　　m:=k MOD l;
　　　　　　k:=l;
　　　　　　l:=m
　　　　　END;
　　　BEGIN
　　　　READ(a,b);
　　　　IF a＜b
　　　　　THEN
　　　　　　okikae(a,b);
　　　　REPEAT
　　　　　amari(a,b)
　　　　UNTIL b=0
　　　　WRITE(a)
　　　END.

11.2　関数

　　関数宣言　＝　関数見出し　”;”　指令　｜　関数表示 ”;”　関数ブロック　｜　関数見出し　”;”　関数ブロック
　　　関数見出し　＝　”FUNCTION”　名称　［　仮引数並び　］”:”　結果型
　　　関数表示　＝　”FUNCTION”　関数名
　　　関数名　＝　名称
　　　結果型　＝　単純型名　｜　ポインタ型名
　　　関数ブロック　＝　ブロック
　　関数は手続きの定義と似ているが、以下の２点が違っている。
　　　（１）関数は値を返すので式の中で用いられる。
　　　（２）関数の仮引数には「VAR」をつけることができない。
　例）
　　FUNCTION gcd(a,b : integer) : integer
　　（１番目の「integer」は仮引数の型を表し、２番目は結果の型を表す。）
　　例４の次の部分を関数の形にしてみる。

　　REPEAT
　　　d:=a MOD b;
　　　a:=b;
　　　b:=d
　　UNTIL d=0
＊関数の形＊
　　FUNCTION gcd(a,b : integer) : integer;
　　　VAR d : integer;
　　　BEGIN
　　　　REPEAT
　　　　　d:=a MOD b;
　　　　　c:=d
　　　　UNTIL d=0;
　　　　gcd:=a
　　　END.

　それでは、この関数を実際にプログラムの中に入れましょう。

　　PROGRAM rei6(input,output);
　　　VAR a,b,kotae : integer;
　　　PROCEDURE okikae(VAR x,y : integer);
　　　　VAR z : integer;
　　　　　BEGIN z:=x; x:=y; y:=z END;
　　FUNCTION gcd(a,b : integer) : integer;
　　　VAR d : integer;
　　　BEGIN
　　　　REPEAT
　　　　　d:=a MOD b;
　　　　　c:=d
　　　　UNTIL d=0;
　　　　gcd:=a
　　　END;
　　BEGIN
　　　READ(a,b);
　　　IF a＜b THEN okikae(a,b);
　　　kotae:=gcd(a,b);
　　　WRITE(kotae)
　　END.

11.3　再帰的

　　「手続きや関数は再帰的な実行ができる。」とは、手続きや関数の中で自分自身の手続きや関数を呼ぶことができるということである。
　　それでは、例として、階乗を計算するプログラムの中の関数の部分を書いてみる。

　　FUNCTION kaijyo(i : integer) : integer;
　　　BEGIN
　　　　IF i＜=0
　　　　　THEN
　　　　　　kaijyo:=1
　　　　　ELSE
　　　　　　kaijyo:=i*kaijyo(i-1)
　　　END;

説明）
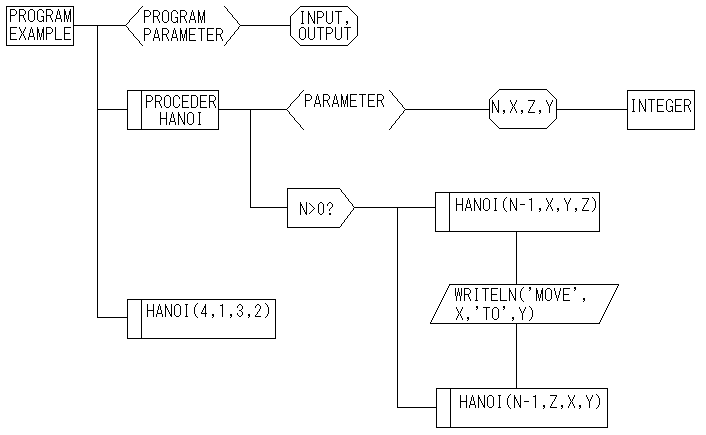
　　（１）kaijyoという名前の関数で仮引数としてのｉが整数型で結果の型を整数とする。
　　（２）IF文でｉの値が０以下なら結果として１を主プログラムに送り、ELSEなら実引数(i-1) が、その前のｉより１小さくなるので、関数が繰り返し自分自身を呼ぶか最後には実引数が１となり、結果を主プログラムに送る。

　　もう１つの例として、「ハノイの塔」のプログラムとそのHichartを示します。
プログラム

　　PROGRAM example(input,output);
　　　PROCEDURE hanoi(VAR n,x,y,z : integer);
　　　　BEGIN
　　　　　IF n＞0
　　　　　　THEN
　　　　　　　BEGIN
　　　　　　　　hanoi(n-1,x,y,z);
　　　　　　　　WRITELN('move',n:5,x:5,'to',y:5);
　　　　　　　　hanoi(n-1,z,x,y)
　　　　　　　END;
　　　　END;
　　　BEGIN
　　　　hanoi(4,1,3,2)
　　　END.

ハノイの塔

練習問題